Naïve Bayesian Classifiers Project & Assignment Help | What is Naive Bayesian Algorithms?
- realcode4you
- Jan 18, 2023
- 2 min read
What is Naive Bayesian Algorithms?
During this lesson the following topics are covered:
Naïve Bayesian Classifier
Theoretical foundations of the classifier
Use cases
Evaluating the effectiveness of the classifier
The Reasons to Choose (+) and Cautions (-) with the use of the classifier
Classification: assign labels to objects.
Usually supervised: training set of pre-classified examples.
Our examples:
Naïve Bayesian
Decision Trees
(and Logistic Regression)
Naïve Bayesian Classifier
- Determine the most probable class label for each object
Based on the observed object attributes
- Naïvely assumed to be conditionally independent of each other
Example:
- Based on the objects attributes {shape, color, weight}
- A given object that is {spherical, yellow, < 60 grams}, may be classified (labeled) as a tennis ball
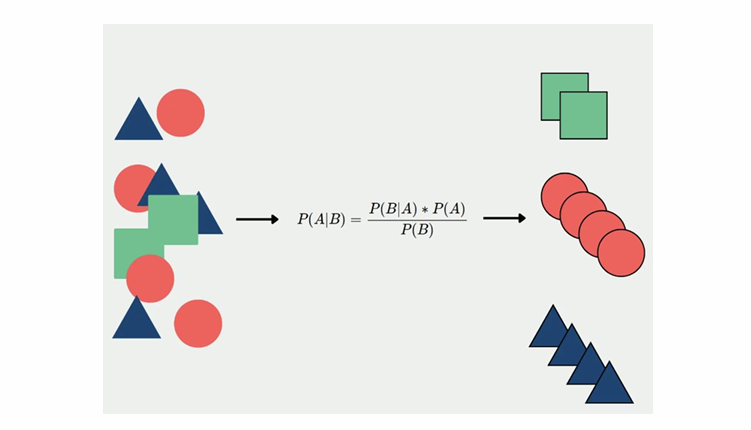
Class label probabilities are determined using Bayes’ Law
- Input variables are discrete
- Output:
Probability score – proportional to the true probability
Class label – based on the highest probability score
Naïve Bayesian Classifier - Use Cases
- Preferred method for many text classification problems.
Try this first; if it doesn't work, try something more complicated
- Use cases
Spam filtering, other text classification tasks
Fraud detection
Technical Description - Bayes' Law

- C is the class label:
C ϵ {C1, C2, … Cn}
- A is the observed object attributes
A = (a1, a2, … am)
- P(C | A) is the probability of C given A is observed
4Called the conditional probability
Apply the Naïve Assumption and Remove a Constant
- For observed attributes A = (a1, a2, … am), we want to compute.

and assign the classifier, Ci, with the largest P(Ci|A).
- Two simplifications to the calculations
Apply naïve assumption - each aj is conditionally independent of each other, then

Denominator P(a1,a2,…am) is a constant and can be ignored.
Building a Naïve Bayesian Classifier
- Applying the two simplifications

- To build a Naïve Bayesian Classifier, collect the following statistics from the training data:
P(Ci) for all the class labels.
P(aj| Ci) for all possible aj and Ci
Assign the classifier label, Ci, that maximizes the value of

Example: Weather data set

Weather data, frequency according to class:





Weather example: solving our example
P(O, T , H, W | Play) = P(O | Play) · P(T | Play). P(H | Play) · P(W | Play)
Weather example when play = Yes or No:
P(Play=Y| x) = P(Play=Y) · [P(O=s| Play=Y) . P(T=c| Play=Y) . P(H=h| Play=Y) . P(W=t| Play=Y)

Weather example when play = Yes:
P(Play=Y| x) = P(Play=Y) · [P(O=s| Play=Y) . P(T=c| Play=Y) . P(H=h| Play=Y) . P(W=t| Play=Y)

Weather example when play = No:
P(Play=N| x) = P(Play=N) · [P(O=s| Play=N) . P(T=c| Play=N) . P(H=h| Play=N) . P(W=t| Play=N)

Hire machine learning experts to get help in all machine learning related algorithms (Linear Regression, Logistic Regression, Decision Tree, K-Means, KNN, etc.).
We are providing you a 10% discount in all coding related assignments. If you are interested in giving assignments to us .We will help you out in the creativity of assignments for further details you may connect with me on WhatsApp and mail using below contact details:
----------------------------------------------------------------------------------------------------------------------
Contact us: +91 82 67 81 38 69
Email us: realcode4you@gmail.com
Visit Here: www.realcode4you.com


Comments