Unsupervised Learning: Clustering | Get Help In Unsupervised Learning Algorithms

Algorithms

• K-means (hard clustering)

• Single Link Clustering (hard clustering)

• Expectation Maximization (soft clustering)

A. K-means Algorithm

1. Assign

• We will choose cluster centers

  • They are called centroids

  • Choosing the initial location of the centroids would affect the final clustering results

2. Optimize

• We will move the cluster centers to minimize the total bands' length

  • The web connects the cluster center to the observations like a spider web

    • So we want to minimize the total length of the web for each centroid

Limitations of K-means

• Suppose you use a fixed number of centroids and training set

  • You would not get the same results

  • It is highly dependent on where you put your centroids initially

    • You might reach a local minima

  • The more centroids you have, the more local minima you will have

B. Single Linkage Clustering (SLC)

• Consider each object a cluster (n objects)

• Define intercluster distance as the distance between the closest two points in the two two clusters

• Merge two closest clusters

• Repeat n-k times to make k clusters

  • In sum, it's just linking up the nearest points

    • Just connect the dots to the nearest dots in a linear fashion

Running Time of SLC

• O(n^3) or slightly lower

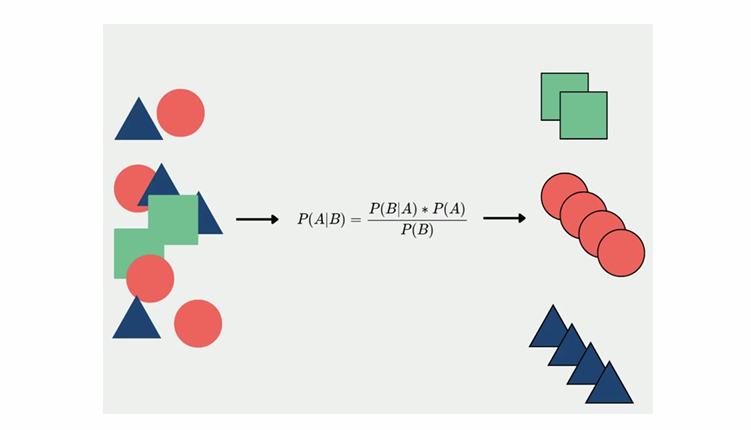
Soft Clustering <br >The idea of 'soft' clustering is that, instead of deciding on definite clusters for each data point, you instead assign each data point a probability that it belongs to one of K clusters.

1. Select one of K Gaussians uniformly

2. Sample x_i from that Gaussian

3. Repeat n times

4. Find a hypothesis that maximizes the probability of the data (maximum likelihood)

C. Expectation Maximization

• The general overview of this is similar to K-means, but instead of judging solely by distance, you are judging by probability, and you are never fully assigning one data point fully to one cluster or one cluster fully to one data point

• You instead assign each point partially to each cluster based on the probability that it would belong to the cluster if you fully knew the clusters, and then assign the mean of each cluster based on the assumption that your prior probabilities were correct, and repeat until you stop getting significant changes

Properties of Expectation Maximization

• Monotonically non-decreasing likelihood

• Does not converge (practically does)

• Will not diverge

• Can get stuck in local optima

  • Solution: randomly restart

• Works with any distribution (if EM solvable)

Clustering Properties <br > No clustering scheme (algorithm) that can achieve all three properties

• Richness

  • For any assignment of objects to clusters, there is some distance matrix D such that P_d, clustering scheme, returns that clustering

    • There are multiple types of clustering

• Scale-invariance

  • Scaling distances by a positive value does not change the clustering

  • Changing units (km to m)

• Consistency

  • Shrinking intracluster distances and expanding intercluster distances does not change the clustering

K-means clustering using scikit-learn

• Hyperparameters available for tuning

  • n_clusters=8

    • This is what you can and should change

  • max_iter=300

    • This determines the number of iterations of:

      1. Assign

      2. Optimize (moving the centroids)

  • n_init=10

    • Number of times to initialize the algorithm

    • If you think your data might need more initializations, you can increase this

Import Libraries

# Imports
import numpy as np
from sklearn.cluster import KMeans
from sklearn import datasets
from sklearn.cross_validation import train_test_split

Split Dataset:

# Set up data
iris = datasets.load_iris()
X = iris.data
y = iris.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.1, random_state=42)

Show Target Data

# Explore target names
iris.target_names

Output

array(['setosa', 'versicolor', 'virginica'], dtype='<U10')

Show Features
# Explore feature names
iris.feature_names

Output

['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']

# Instantiate
kmc = KMeans(n_clusters=3, max_iter=1000, n_init=20)

# Fit
kmc.fit(X_train, y_train)

Output

KMeans(copy_x=True, init='k-means++', max_iter=1000, n_clusters=3, n_init=20, n_jobs=1, precompute_distances='auto', random_state=None, tol=0.0001, verbose=0)