Ensemble Learning and Random Forests Assignment Help | What is Ensemble Learning?
- realcode4you
- Feb 26, 2022
- 15 min read
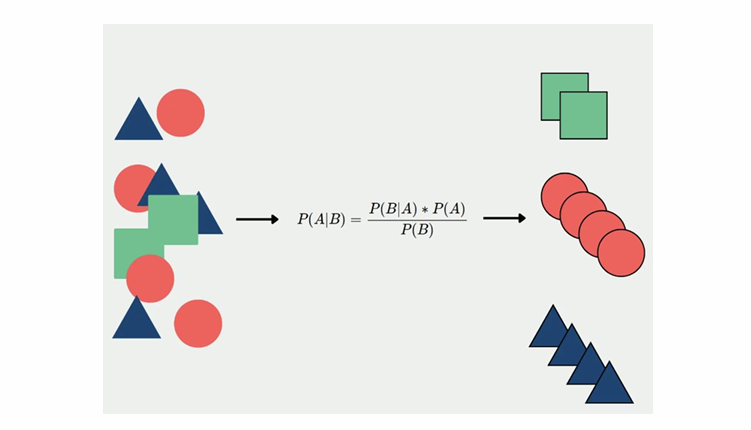
Suppose you pose a complex question to thousands of random people, then aggregate their answers. In many cases you will find that this aggregated answer is better than an expert’s answer. This is called the wisdom of the crowd. Similarly, if you aggregate the predictions of a group of predictors (such as classifiers or regressors), you will often get better predictions than with the best individual predictor. A group of predictors is called an ensemble; thus, this technique is called Ensemble Learning, and an Ensemble Learning algorithm is called an Ensemble method.
As an example of an Ensemble method, you can train a group of Decision Tree classifiers, each on a different random subset of the training set. To make predictions, you obtain the predictions of all the individual trees, then predict the class that gets the most votes. Such an ensemble of Decision Trees is called a Random Forest, and despite its simplicity, this is one of the most powerful Machine Learning algorithms available today.
You will often use Ensemble methods near the end of a project, once you have already built a few good predictors, to combine them into an even better predictor. In fact, the winning solutions in Machine Learning competitions often involve several Ensemble methods (most famously in the Netflix Prize competition).
In this module we will discuss the most popular Ensemble methods, including bagging, boosting, and stacking. We will also explore Random Forests.
Bagging and Pasting
One way to get a diverse set of classifiers is to use very different training algorithms, as just discussed. Another approach is to use the same training algorithm for every predictor and train them on different random subsets of the training set. When sampling is performed with replacement, this method is called bagging (short for boot-strap aggregating). When sampling is performed without replacement, it is called pasting.
In other words, both bagging and pasting allow training instances to be sampled several times across multiple predictors, but only bagging allows training instances to be sampled several times for the same predictor. This sampling and training process is represented in the following figure.

Once all predictors are trained, the ensemble can make a prediction for a new instance by simply aggregating the predictions of all predictors. The aggregation function is typically the statistical mode (i.e., the most frequent prediction, just like a hard voting classifier) for classification, or the average for regression. Each individual predictor has a higher bias than if it were trained on the original training set, but aggregation reduces both bias and variance. Generally, the net result is that the ensemble has a similar bias but a lower variance than a single predictor trained on the original training set.
As you can see in the above figure, predictors can all be trained in parallel, via different CPU cores or even different servers. Similarly, predictions can be made in parallel. This is one of the reasons bagging and pasting are such popular methods: they scale very well.
Bagging and Pasting
In Scikit-Learn Scikit-Learn offers a simple API for both bagging and pasting with the BaggingClassifier class (or BaggingRegressor for regression). The following code trains an ensemble of 500 Decision Tree classifiers: each is trained on 100 training instances randomly sampled from the training set with replacement (this is an example of bagging, but if you want to use pasting instead, just set bootstrap=False). The n_jobs parameter tells Scikit-Learn the number of CPU cores to use for training and predictions (–1 tells Scikit-Learn to use all available cores):
from sklearn.ensemble import BaggingClassifier
from sklearn.tree import DecisionTreeClassifier
bag_clf = BaggingClassifier( DecisionTreeClassifier(), n_estimators=500, max_samples=100, bootstrap=True, n_jobs=-1)
bag_clf.fit(X_train, y_train)
y_pred = bag_clf.predict(X_test) The BaggingClassifier automatically performs soft voting instead of hard voting if the base classifier can estimate class probabilities (i.e., if it has a predict_proba() method), which is the case with Decision Tree classifiers.
The following figure compares the decision boundary of a single Decision Tree with the decision boundary of a bagging ensemble of 500 trees (from the preceding code), both trained on the moons dataset. As you can see, the ensemble’s predictions will likely generalize much better than the single Decision Tree’s predictions: the ensemble has a comparable bias but a smaller variance (it makes roughly the same number of errors on the training set, but the decision boundary is less irregular).

Bootstrapping introduces a bit more diversity in the subsets that each predictor is trained on, so bagging ends up with a slightly higher bias than pasting; but the extra diversity also means that the predictors end up being less correlated, so the ensemble’s variance is reduced. Overall, bagging often results in better models, which explains why it is generally preferred. However, if you have spare time and CPU power, you can use cross-validation to evaluate both bagging and pasting and select the one that works best.
Out-of-Bag Evaluation
With bagging, some instances may be sampled several times for any given predictor, while others may not be sampled at all. By default a BaggingClassifier samples m training instances with replacement (bootstrap=True), where m is the size of the training set. This means that only about 63% of the training instances are sampled on average for each predictor. The remaining 37% of the training instances that are not sampled are called out-of-bag (oob) instances. Note that they are not the same 37% for all predictors.
Since a predictor never sees the oob instances during training, it can be evaluated on these instances, without the need for a separate validation set. You can evaluate the ensemble itself by averaging out the oob evaluations of each predictor.
In Scikit-Learn, you can set oob_score=True when creating a BaggingClassifier to request an automatic oob evaluation after training. The following code demonstrates this. The resulting evaluation score is available through the oob_score_ variable:
bag_clf = BaggingClassifier( DecisionTreeClassifier(), n_estimators=500, bootstrap=True, n_jobs=-1, oob_score=True)
bag_clf.fit(X_train, y_train)
bag_clf.oob_score_According to this oob evaluation, this BaggingClassifier is likely to achieve about 89.9% accuracy on the test set. Let’s verify this:
from sklearn.metrics import accuracy_score
y_pred = bag_clf.predict(X_test)
accuracy_score(y_test, y_pred) We get 91.2% accuracy on the test set—close enough!
The oob decision function for each training instance is also available through the oob_decision_function_ variable. In this case (since the base estimator has a predict_proba() method), the decision function returns the class probabilities for each training instance. For example, the oob evaluation estimates that the first training instance has a 67.7% probability of belonging to the positive class (and 32.3% of belonging to the negative class):
bag_clf.oob_decision_function_ Random Patches and Random Subspaces
The BaggingClassifier class supports sampling the features as well. Sampling is controlled by two hyperparameters: max_features and bootstrap_features. They work the same way as max_samples and bootstrap, but for feature sampling instead of instance sampling. Thus, each predictor will be trained on a random subset of the input features.
This technique is particularly useful when you are dealing with high-dimensional inputs (such as images). Sampling both training instances and features is called the Random Patches method. Keeping all training instances (by setting bootstrap=False and max_samples=1.0) but sampling features (by setting bootstrap_features to True and/or max_features to a value smaller than 1.0) is called the Random Subspaces method.
Sampling features results in even more predictor diversity, trading a bit more bias for a lower variance.
Random Forests
As we have discussed, a Random Forest is an ensemble of Decision Trees, generally trained via the bagging method (or sometimes pasting), typically with max_samples set to the size of the training set. Instead of building a BaggingClassifier and passing it a DecisionTreeClassifier, you can instead use the RandomForestClassifier class, which is more convenient and optimized for Decision Trees (similarly, there is a RandomForestRegressor class for regression tasks). The following code uses all available CPU cores to train a Random Forest classifier with 500 trees (each limited to maximum 16 nodes):
from sklearn.ensemble import RandomForestClassifier
rnd_clf = RandomForestClassifier(n_estimators=500, max_leaf_nodes=16, n_jobs=-1) rnd_clf.fit(X_train, y_train)
y_pred_rf = rnd_clf.predict(X_test)With a few exceptions, a RandomForestClassifier has all the hyperparameters of a DecisionTreeClassifier (to control how trees are grown), plus all the hyperparameters of a BaggingClassifier to control the ensemble itself. The Random Forest algorithm introduces extra randomness when growing trees; instead of searching for the very best feature when splitting a node (recall this is done for decision trees), it searches for the best feature among a random subset of features. The algorithm results in greater tree diversity, which (again) trades a higher bias for a lower variance, generally yielding an overall better model. The following BaggingClassifier is roughly equivalent to the previous RandomForestClassifier:
bag_clf = BaggingClassifier( DecisionTreeClassifier(splitter="random", max_leaf_nodes=16), n_estimators=500, max_samples=1.0, bootstrap=True, n_jobs=-1) Extra-Trees
When you are growing a tree in a Random Forest, at each node only a random subset of the features is considered for splitting (as discussed earlier). It is possible to make trees even more random by also using random thresholds for each feature rather than searching for the best possible thresholds (like regular Decision Trees do).
A forest of such extremely random trees is called an Extremely Randomized Trees ensemble (or Extra-Trees for short). Once again, this technique trades more bias for a lower variance. It also makes Extra-Trees much faster to train than regular Random Forests, because finding the best possible threshold for each feature at every node is one of the most time-consuming tasks of growing a tree.
You can create an Extra-Trees classifier using Scikit-Learn’s ExtraTreesClassifier class. Its API is identical to the RandomForestClassifier class. Similarly, the ExtraTreesRegressor class has the same API as the RandomForestRegressor class.
It is hard to tell in advance whether a RandomForestClassifier will perform better or worse than an ExtraTreesClassifier. Generally, the only way to know is to try both and compare them using cross-validation (tuning the hyperparameters using grid search).
Feature Importance
Yet another great quality of Random Forests is that they make it easy to measure the relative importance of each feature. Scikit-Learn measures a feature’s importance by looking at how much the tree nodes that use that feature reduce impurity on average (across all trees in the forest). More precisely, it is a weighted average, where each node’s weight is equal to the number of training samples that are associated with it.
Scikit-Learn computes this score automatically for each feature after training, then it scales the results so that the sum of all importances is equal to 1. You can access the result using the feature_importances_ variable. For example, the following code trains a RandomForestClassifier on the iris dataset and outputs each feature’s importance. It seems that the most important features are the petal length (44%) and width (42%), while sepal length and width are rather unimportant in comparison (11% and 2%, respectively):
from sklearn.datasets import load_iris
iris = load_iris()
rnd_clf = RandomForestClassifier(n_estimators=500, n_jobs=-1)
rnd_clf.fit(iris["data"], iris["target"]) for name, score in zip(iris["feature_names"] Similarly, if you train a Random Forest classifier on the MNIST dataset and plot each pixel’s importance, you get the image represented in the following figure.

Random Forests are very handy to get a quick understanding of what features actually matter, in particular if you need to perform feature selection.
Boosting
Boosting refers to any Ensemble method that can combine several weak learners into a strong learner. The general idea of most boosting methods is to train predictors sequentially, each trying to correct its predecessor. There are many boosting methods available, but by far the most popular are AdaBoost (short for Adaptive Boosting) and Gradient Boosting. Let’s start with AdaBoost.
AdaBoost
One way for a new predictor to correct its predecessor is to pay a bit more attention to the training instances that the predecessor underfit. This results in new predictors focusing more and more on the hard cases. This is the technique used by AdaBoost. For example, when training an AdaBoost classifier, the algorithm first trains a base classifier (such as a Decision Tree) and uses it to make predictions on the training set. The algorithm then increases the relative weight of misclassified training instances. Then it trains a second classifier, using the updated weights, and again makes predictions on the training set, updates the instance weights, and so on (see the following figure).

The following code trains an AdaBoost classifier based on 200 Decision Stumps using Scikit-Learn’s AdaBoostClassifier class (as you might expect, there is also an Ada BoostRegressor class). A Decision Stump is a Decision Tree with max_depth=1 - in other words, a tree composed of a single decision node plus two leaf nodes. This is the default base estimator for the AdaBoostClassifier class:
from sklearn.ensemble import AdaBoostClassifier
ada_clf = AdaBoostClassifier( DecisionTreeClassifier(max_depth=1), n_estimators=200, algorithm="SAMME.R", learning_rate=0.5)
ada_clf.fit(X_train, y_train)If your AdaBoost ensemble is overfitting the training set, you can try reducing the number of estimators or more strongly regularizing the base estimator.
The following figure shows the decision boundaries of five consecutive predictors trained on the moons dataset (in this example, each predictor is a highly regularized SVM classifier with an RBF kernel). This code illustrates a custom implementation that is similar to the AdaBoost algorithm, but not identical. The first classifier gets many instances wrong, so their weights get boosted. The second classifier therefore does a better job on these instances, and so on. The plot on the right represents the same sequence of predictors, except that the learning rate is halved (i.e., the misclassified instance weights are boosted half as much at every iteration). As you can see, this sequential learning technique has some similarities with Gradient Descent, except that instead of tweaking a single predictor’s parameters to minimize a cost function, AdaBoost adds predictors to the ensemble, gradually making it better.

Once all predictors are trained, the ensemble makes predictions very much like bagging or pasting, except that predictors have different weights depending on their overall accuracy on the weighted training set.
There is one important drawback to this sequential learning technique: it cannot be parallelized (or only partially), since each predictor can only be trained after the previous predictor has been trained and evaluated. As a result, it does not scale as well as bagging or pasting.
Let’s take a closer look at the AdaBoost algorithm. Each instance weight w is initially set to 1/m. A first predictor is trained, and its weighted error rate r is computed on the training set; see the following equation.

The predictor’s weight αj is then computed using the following equation, where η is the learning rate hyperparameter (defaults to 1). The more accurate the predictor is, the higher its weight will be. If it is just guessing randomly, then its weight will be close to zero. However, if it is most often wrong (i.e., less accurate than random guessing), then its weight will be negative.

Next, the AdaBoost algorithm updates the instance weights, using the following equation, which boosts the weights of the misclassified instances.

Finally, a new predictor is trained using the updated weights, and the whole process is repeated (the new predictor’s weight is computed, the instance weights are updated, then another predictor is trained, and so on). The algorithm stops when the desired number of predictors is reached, or when a perfect predictor is found.
To make predictions, AdaBoost simply computes the predictions of all the predictors and weighs them using the predictor weights αj. The predicted class is the one that receives the majority of weighted votes (see the following equation).

Scikit-Learn uses a multiclass version of AdaBoost called SAMME (which stands for Stagewise Additive Modeling using a Multiclass Exponential loss function). When there are just two classes, SAMME is equivalent to AdaBoost. If the predictors can estimate class probabilities (i.e., if they have a predict_proba() method), Scikit-Learn can use a variant of SAMME called SAMME.R (the R stands for “Real”), which relies on class probabilities rather than predictions and generally performs better.
Gradient Boosting
Another very popular boosting algorithm is Gradient Boosting. Just like AdaBoost, Gradient Boosting works by sequentially adding predictors to an ensemble, each one correcting its predecessor. However, instead of tweaking the instance weights at every iteration like AdaBoost does, this method tries to fit the new predictor to the residual errors made by the previous predictor.

Let’s go through a simple regression example, using Decision Trees as the base predictors (of course, Gradient Boosting also works great with classification tasks). This is called Gradient Tree Boosting, or Gradient Boosted Regression Trees (GBRT). First, let’s fit a DecisionTreeRegressor to the training set (for example, a noisy quadratic training set):
from sklearn.tree import DecisionTreeRegressor
tree_reg1 = DecisionTreeRegressor(max_depth=2) tree_reg1.fit(X, y)Next, we’ll train a second DecisionTreeRegressor on the residual errors made by the first predictor:
y2 = y - tree_reg1.predict(X)
tree_reg2 = DecisionTreeRegressor(max_depth=2)
tree_reg2.fit(X, y2)Then we train a third regressor on the residual errors made by the second predictor:
y3 = y2 - tree_reg2.predict(X)
tree_reg3 = DecisionTreeRegressor(max_depth=2)
tree_reg3.fit(X, y3) Now we have an ensemble containing three trees. It can make predictions on a new instance simply by adding up the predictions of all the trees.
y_pred = sum(tree.predict(X_new) for tree in (tree_reg1, tree_reg2, tree_reg3)) The following figure represents the predictions of these three trees in the left column, and the ensemble’s predictions in the right column. In the first row, the ensemble has just one tree, so its predictions are exactly the same as the first tree’s predictions. In the second row, a new tree is trained on the residual errors of the first tree. On the right you can see that the ensemble’s predictions are equal to the sum of the predictions of the first two trees. Similarly, in the third row another tree is trained on the residual errors of the second tree. You can see that the ensemble’s predictions gradually get better as trees are added to the ensemble.

A simpler way to train GBRT ensembles is to use Scikit-Learn’s GradientBoostingRegressor class. Much like the RandomForestRegressor class, it has hyperparameters to control the growth of Decision Trees (e.g., max_depth, min_samples_leaf), as well as hyperparameters to control the ensemble training, such as the number of trees (n_estimators). The following code creates the same ensemble as the previous one:
from sklearn.ensemble import GradientBoostingRegressor
gbrt = GradientBoostingRegressor(max_depth=2, n_estimators=3, learning_rate=1.0) gbrt.fit(X, y) The learning_rate hyperparameter scales the contribution of each tree. If you set it to a low value, such as 0.1, you will need more trees in the ensemble to fit the training set, but the predictions will usually generalize better. This is a regularization technique called shrinkage. The following figure shows two GBRT ensembles trained with a low learning rate: the one on the left does not have enough trees to fit the training set, while the one on the right has too many trees and overfits the training set.

Early Stopping
In order to find the optimal number of trees, you can use early stopping. A simple way to implement this is to use the staged_predict() method: it returns an iterator over the predictions made by the ensemble at each stage of training (with one tree, two trees, etc.). The following code trains a GBRT ensemble with 120 trees, then measures the validation error at each stage of training to find the optimal number of trees, and finally trains another GBRT ensemble using the optimal number of trees:
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
X_train, X_val, y_train, y_val = train_test_split(X, y)
gbrt = GradientBoostingRegressor(max_depth=2, n_estimators=120)
gbrt.fit(X_train, y_train) errors = [mean_squared_error(y_val, y_pred) for y_pred in gbrt.staged_predict(X_val)] bst_n_estimators = np.argmin(errors) + 1
gbrt_best = GradientBoostingRegressor(max_depth=2,n_estimators=bst_n_estimators) gbrt_best.fit(X_train, y_train) The validation errors are represented on the left of the following figure, and the best model’s predictions are represented on the right.

It is also possible to implement early stopping by actually stopping training early (instead of training a large number of trees first and then looking back to find the optimal number). You can do so by setting warm_start=True, which makes Scikit-Learn keep existing trees when the fit() method is called, allowing incremental training. The following code stops training when the validation error does not improve for five iterations in a row:

The GradientBoostingRegressor class also supports a subsample hyperparameter, which specifies the fraction of training instances to be used for training each tree. For example, if subsample = 0.25, then each tree is trained on 25% of the training instances, selected randomly. As you can probably guess by now, this technique trades a higher bias for a lower variance. It also speeds up training considerably. This is called Stochastic Gradient Boosting.
It is possible to use Gradient Boosting with other cost functions. This is controlled by the loss hyperparameter (see Scikit-Learn’s documentation for more details).
It is worth noting that an optimized implementation of Gradient Boosting is available in the popular Python library XGBoost, which stands for Extreme Gradient Boosting. This package was initially developed as part of the Distributed (Deep) Machine Learning Community (DMLC), and it aims to be extremely fast, scalable, and portable. In fact, XGBoost is often an important component of the winning entries in ML competitions. XGBoost’s API is quite similar to Scikit-Learn’s:
import xgboost
xgb_reg = xgboost.XGBRegressor()
xgb_reg.fit(X_train, y_train)
y_pred = xgb_reg.predict(X_val)XGBoost also offers several nice features, such as automatically taking care of early stopping:
xgb_reg.fit(X_train, y_train, eval_set=[(X_val, y_val)], early_stopping_rounds=2)
y_pred = xgb_reg.predict(X_val) You should definitely check it out!
Stacking
The last Ensemble method we will discuss in this chapter is called stacking (short for stacked generalization). It is based on a simple idea: instead of using trivial functions (such as hard voting) to aggregate the predictions of all predictors in an ensemble, why don’t we train a model to perform this aggregation? The following figure shows such an ensemble performing a regression task on a new instance. Each of the bottom three predictors predicts a different value (3.1, 2.7, and 2.9), and then the final predictor (called a blender, or a meta learner) takes these predictions as inputs and makes the final prediction (3.0).

To train the blender, a common approach is to use a hold-out set. Let’s see how it works. First, the training set is split into two subsets. The first subset is used to train the predictors in the first layer (see following figure).

Next, the first layer’s predictors are used to make predictions on the second (held-out) set (see the following figure). This ensures that the predictions are “clean,” since the predictors never saw these instances during training. For each instance in the hold-out set, there are three predicted values. We can create a new training set using these predicted values as input features (which makes this new training set 3D), and keeping the target values. The blender is trained on this new training set, so it learns to predict the target value, given the first layer’s predictions.

It is actually possible to train several different blenders this way (e.g., one using Linear Regression, another using Random Forest Regression), to get a whole layer of blenders. The trick is to split the training set into three subsets: the first one is used to train the first layer, the second one is used to create the training set used to train the second layer (using predictions made by the predictors of the first layer), and the third one is used to create the training set to train the third layer (using predictions made by the predictors of the second layer). Once this is done, we can make a prediction for a new instance by going through each layer sequentially, as shown in the following figure.

Unfortunately, Scikit-Learn does not support stacking directly, but it is not too hard to roll out your own implementation. Alternatively, you can use an open source implementation such as DESlib.
If you have any query then comment in below comment section or need any help related to this topics then we are ready to help you. Send your requirement details at:
realcode4you@gmail.com


Comments