Supervised Machine Learning Algorithms Help |Important Supervised Algorithms
- realcode4you
- Sep 21, 2021
- 7 min read
In this blog we have covers all supervised Learning algorithms code implementation, there are many types of supervised learning algorithms as per below:
K-NN Classification
Naive Bayes Classifier
Random Forest
At last we will learn about "Distance"
K-NN Classification
To be able to illustrate how we perform kNN classification in Python, we need some data first. Therefore we synthesize some data from 3 classes. We assume the data in each class comes from a multivariate random distribution.
Import Libraries
#import Libraries
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
sns.set()np.random.seed(100)
n_per_class = 50
colors = ['green', 'blue', 'magenta']
mean1 = [-5, 10]
cov1 = [[1.5, 0], [0, 1.5]]
mean2 = [0, 7]
cov2 = [[1.5, 0], [0, 3]]
mean3 = [-6, 6]
cov3 = [[2, 0], [0, 1.5]]
means = [mean1, mean2, mean3]
covs = [cov1, cov2, cov3]
x11, x12 = np.random.multivariate_normal(means[0], covs[0], n_per_class).T
x21, x22 = np.random.multivariate_normal(means[1], covs[1], n_per_class).T
x31, x32 = np.random.multivariate_normal(means[2], covs[2], n_per_class).T
scale = 75
alpha = 0.6
fig, ax = plt.subplots(figsize=(7, 7), dpi=300)
ax.scatter(x11, x12, alpha=alpha, color=colors[0], s=scale)
ax.scatter(x21, x22, alpha=alpha, color=colors[1], s=scale)
ax.scatter(x31, x32, alpha=alpha, color=colors[2], s=scale)
ax.set_title("synthesized data for 3 classes")
ax.set_xlabel("$x_1$")
ax.set_ylabel("$x_2$")Output:

Then we have to instantiate a kNN classifier from sklearn.
from sklearn import neighbors
weights='uniform'
k = 15
knn = neighbors.KNeighborsClassifier(k,weights=weights)
We need to pass one array as training features and on array as training labels to the knn object. Therefore we have to put all the attributes together (also class labels).
x1 = np.r_[x11, x21, x31]
x2 = np.r_[x12, x22, x32]
X_train = np.c_[x1, x2]Y_train = np.r_[0*np.ones(n_per_class), 1*np.ones(n_per_class), 2*np.ones(n_per_class)]Now we can fit the model
knn.fit(X_train, Y_train)Now we will see how kNN classifies a point.
k = 1
knn = neighbors.KNeighborsClassifier(k)
knn.fit(X_train, Y_train)from matplotlib.colors import ListedColormap
cmap_bold = ListedColormap(['green', 'blue', 'magenta'])fig,ax = plt.subplots(figsize=(7, 7))
ax.scatter(X_train[:, 0], X_train[:, 1], c=Y_train, cmap=cmap_bold, alpha=alpha, s=scale)
plt.title("3-Class classification (k = {})".format(k))
X_test = [-7, 10]
Y_pred = knn.predict(X_test)
ax.scatter(X_test[0], X_test[1], marker="x", s=scale, lw=2, c='k')
ax.set_title("3-Class classification (k = {})\n Red point is predicted as class {}".format(k, colors[Y_pred.astype(int)[0]]))Decision Boundry kNN effectively partitions the feature space into different sets and assigns the same class label to points belonging to the same partition. This partitioning changes as we change k. We illustrate this below. As you see bigger values of k, partition the space more smoothly.
from matplotlib.colors import ListedColormapk = 15
knn = neighbors.KNeighborsClassifier(k, weights=weights)
knn.fit(X_train, Y_train)
# step size in the mesh
h = 0.05
# Create colour maps
cmap_light = ListedColormap(['#AAFFAA', '#AAAAFF', '#FFAAAA'])
cmap_bold = ListedColormap(['green', 'blue', 'magenta'])
x1_min, x1_max = X_train[:, 0].min() - 1, X_train[:, 0].max() + 1
x2_min, x2_max = X_train[:, 1].min() - 1, X_train[:, 1].max() + 1
xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, h), np.arange(x2_min, x2_max, h))
Z = knn.predict(np.c_[xx1.ravel(), xx2.ravel()])
# Put the result into a color plot
Z = Z.reshape(xx1.shape)
fig,ax = plt.subplots(figsize=(7, 7))
ax.pcolormesh(xx1, xx2, Z, cmap=cmap_light)
# Plot also the training points
ax.scatter(X_train[:, 0], X_train[:, 1], c=Y_train, cmap=cmap_bold, alpha=alpha, s=scale)
plt.xlim(xx1.min(), xx1.max())
plt.ylim(xx2.min(), xx2.max())
plt.title("3-Class classification (k = {})".format(k))Output:

Now we will investigate the effect of 'k' on decision boundaries. Lets train a classifier with k=1 which means we only use the label of the closest point to predict the label of a test point.
k = 1
knn = neighbors.KNeighborsClassifier(k, weights=weights)
knn.fit(X_train, Y_train)
Z = knn.predict(np.c_[xx1.ravel(), xx2.ravel()])
Z = Z.reshape(xx1.shape)
fig,ax = plt.subplots(figsize=(7, 7))
ax.pcolormesh(xx1, xx2, Z, cmap=cmap_light)
ax.scatter(X_train[:, 0], X_train[:, 1], c=Y_train, cmap=cmap_bold, alpha=alpha, s=scale)
plt.xlim(xx1.min(), xx1.max())
plt.ylim(xx2.min(), xx2.max())
plt.title("3-Class classification (k = {})".format(k))Output:

k = 2
knn = neighbors.KNeighborsClassifier(k, weights=weights)
knn.fit(X_train, Y_train)
Z = knn.predict(np.c_[xx1.ravel(), xx2.ravel()])
Z = Z.reshape(xx1.shape)
fig,ax = plt.subplots(figsize=(7, 7))
ax.pcolormesh(xx1, xx2, Z, cmap=cmap_light)
ax.scatter(X_train[:, 0], X_train[:, 1], c=Y_train, cmap=cmap_bold, alpha=alpha, s=scale)
plt.xlim(xx1.min(), xx1.max())
plt.ylim(xx2.min(), xx2.max())
plt.title("3-Class classification (k = {})".format(k))Output:

k = 3
knn = neighbors.KNeighborsClassifier(k, weights=weights)
knn.fit(X_train, Y_train)
Z = knn.predict(np.c_[xx1.ravel(), xx2.ravel()])
Z = Z.reshape(xx1.shape)
fig,ax = plt.subplots(figsize=(7, 7))
ax.pcolormesh(xx1, xx2, Z, cmap=cmap_light)
ax.scatter(X_train[:, 0], X_train[:, 1], c=Y_train, cmap=cmap_bold, alpha=alpha, s=scale)
plt.xlim(xx1.min(), xx1.max())
plt.ylim(xx2.min(), xx2.max())
plt.title("3-Class classification (k = {})".format(k))Output:

k = 5
knn = neighbors.KNeighborsClassifier(k, weights=weights)
knn.fit(X_train, Y_train)
Z = knn.predict(np.c_[xx1.ravel(), xx2.ravel()])
Z = Z.reshape(xx1.shape)
fig,ax = plt.subplots(figsize=(7, 7))
ax.pcolormesh(xx1, xx2, Z, cmap=cmap_light)
ax.scatter(X_train[:, 0], X_train[:, 1], c=Y_train, cmap=cmap_bold, alpha=alpha, s=scale)
plt.xlim(xx1.min(), xx1.max())
plt.ylim(xx2.min(), xx2.max())
plt.title("3-Class classification (k = {})".format(k))Output:

Prediction
k = 5
knn = neighbors.KNeighborsClassifier(k, weights=weights)
knn.fit(X_train, Y_train)
Z = knn.predict(np.c_[xx1.ravel(), xx2.ravel()])
Z = Z.reshape(xx1.shape)
fig,ax = plt.subplots(figsize=(7, 7))
ax.pcolormesh(xx1, xx2, Z, cmap=cmap_light)
ax.scatter(X_train[:, 0], X_train[:, 1], c=Y_train, cmap=cmap_bold, alpha=alpha, s=scale)
plt.xlim(xx1.min(), xx1.max())
plt.ylim(xx2.min(), xx2.max())
plt.title("3-Class classification (k = {})".format(k))
X_test = [-4, 8]
Y_pred = knn.predict(X_test)
ax.scatter(X_test[0], X_test[1], alpha=0.95, color='r', s=3*scale)
ax.set_title("3-Class classification (k = {})\n Red point is predicted as class {}".format(k, colors[Y_pred.astype(int)[0]]))Now instead of predicting the class label for one point, we use our model to predict the labels of multiple points.
First we generate some test data from the first class. This way we know the true class labels. Then we can use the kNN classifier to predict labels for the test data and get the predicted class labels. A measure of accuracy for the classifier can be defined by comparing the true and predicted labels.
n_test = 100
X1_test, X2_test = np.random.multivariate_normal(mean1, cov1, n_test).T
Y_true = 0 * np.ones(n_test)
X_test = np.c_[X1_test, X2_test]
Y_pred = knn.predict(X_test)
Y_pred
Y_pred == Y_true
(sum(Y_pred == Y_true) + 0.0) / n_testNaive Bayes Classifier
Naive Bayes is one of the most practical classification machine learning algorithms.
fast
good performance
simple yet very effective
robust to irrelative features
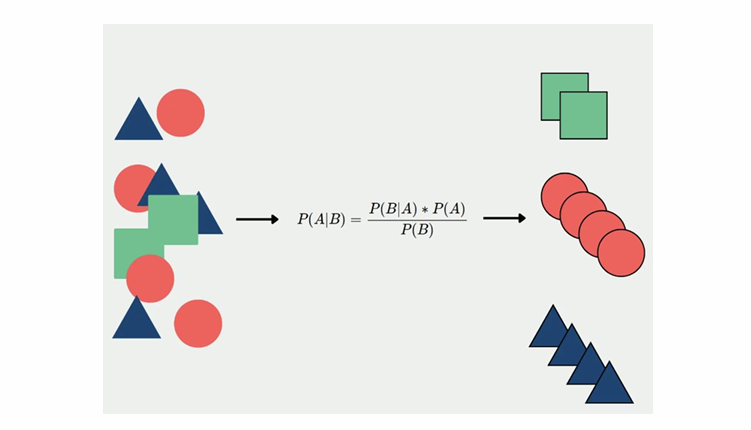
So why is it called naive?
Because it does not consider the dependency between features and assume all features are independent of each other which is not the case in reality. This is a naive assumption, hence the name.
The accuracy is very good although this naive assumption. A famous example of NB usage is spam filtering.
NBC by Example
We assume we have collected the below data for the past 5 days. Based on this data, can we predict if our subject will play in a setting like:
outlook = overcast
temp = hot
humidity = normal
windy = no
from __future__ import division
import numpy as np
import pandas as pddata = {
'outlook': [0, 1, 2, 0, 1],
'temp' : [0, 1, 2, 1, 0],
'humid' : [0, 0, 1, 0, 1],
'wind' : [0, 0, 1, 1, 0],
'play' : [1, 1, 0, 0, 0,]
}
df = pd.DataFrame(data)Output:

def marginal_prob(df, col):
ll = [(ss, (df[col] == ss).sum()) for ss in set(df[col])]
total_count = [b for a,b in ll]
total_count = sum(total_count)
ll2 = [(a, b/total_count) for a, b in ll]
return dict(ll2)To calculate probability of a feature given the class (play) we use conditinoal probability.
def conditional_prob(df, f, c, val):
df2 = df[df[c] == val][f]
ll = [[ss, (df2 == ss).sum()] for ss in set(df2)]
total_count = [b for a,b in ll]
total_count = sum(total_count)
ll2 = [(a, b/total_count) for a, b in ll]
return dict(ll2)Now we can use Bayes rule:
o = 1
t = 0
h = 0
w = 0
c = 0
p0 = marginal_prob(df, 'play')[c] * conditional_prob(df, 'outlook', 'play', c)[o] * conditional_prob(df, 'temp', 'play', c)[t] \
* conditional_prob(df, 'humid', 'play', c)[h] * conditional_prob(df, 'wind', 'play', c)[w]
c = 1
p1 = marginal_prob(df, 'play')[c] * conditional_prob(df, 'outlook', 'play', c)[o] * conditional_prob(df, 'temp', 'play', c)[t] \
* conditional_prob(df, 'humid', 'play', c)[h] * conditional_prob(df, 'wind', 'play', c)[w]
# normalizing
p_sum = p0 + p1
p0 /= p_sum
p1 /= p_sum
print "probability of not playing: {}".format(p0)
print "probability of playing : {}".format(p1)Decision Tree
Here's an example of a decision tree classifier in scikit-learn. We'll start by defining some two-dimensional labeled data:
from sklearn.datasets import make_blobs
X, y = make_blobs(n_samples=300, centers=4,
random_state=0, cluster_std=1.0)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='rainbow');# We have some convenience functions in the repository that help
from fig_code import visualize_tree, plot_tree_interactive
# Now using IPython's ``interact`` (available in IPython 2.0+, and requires a live kernel) we can view the decision tree splits:
plot_tree_interactive(X, y);
Notice that at each increase in depth, every node is split in two except those nodes which contain only a single class. The result is a very fast non-parametric classification, and can be extremely useful in practice.
Question: Do you see any problems with this?
Decision Trees and over-fitting
One issue with decision trees is that it is very easy to create trees which over-fit the data. That is, they are flexible enough that they can learn the structure of the noise in the data rather than the signal! For example, take a look at two trees built on two subsets of this dataset:
from sklearn.tree import DecisionTreeClassifier
clf = DecisionTreeClassifier()
plt.figure()
visualize_tree(clf, X[:200], y[:200], boundaries=False)
plt.figure()
visualize_tree(clf, X[-200:], y[-200:], boundaries=False)
The details of the classifications are completely different! That is an indication of over-fitting: when you predict the value for a new point, the result is more reflective of the noise in the model rather than the signal.
Ensembles of Estimators: Random Forests
One possible way to address over-fitting is to use an Ensemble Method: this is a meta-estimator which essentially averages the results of many individual estimators which over-fit the data. Somewhat surprisingly, the resulting estimates are much more robust and accurate than the individual estimates which make them up!
One of the most common ensemble methods is the Random Forest, in which the ensemble is made up of many decision trees which are in some way perturbed.
There are volumes of theory and precedent about how to randomize these trees, but as an example, let's imagine an ensemble of estimators fit on subsets of the data. We can get an idea of what these might look like as follows
def fit_randomized_tree(random_state=0):
X, y = make_blobs(n_samples=300, centers=4,
random_state=0, cluster_std=2.0)
clf = DecisionTreeClassifier(max_depth=15)
rng = np.random.RandomState(random_state)
i = np.arange(len(y))
rng.shuffle(i)
visualize_tree(clf, X[i[:250]], y[i[:250]], boundaries=False,
xlim=(X[:, 0].min(), X[:, 0].max()),
ylim=(X[:, 1].min(), X[:, 1].max()))
from IPython.html.widgets import interact
interact(fit_randomized_tree, random_state=[0, 100]);
See how the details of the model change as a function of the sample, while the larger characteristics remain the same! The random forest classifier will do something similar to this, but use a combined version of all these trees to arrive at a final answer:
from sklearn.ensemble import RandomForestClassifier
clf = RandomForestClassifier(n_estimators=100, random_state=0, n_jobs=-1)
visualize_tree(clf, X, y, boundaries=False);By averaging over 100 randomly perturbed models, we end up with an overall model which is a much better fit to our data!
(Note: above we randomized the model through sub-sampling... Random Forests use more sophisticated means of randomization, which you can read about in, e.g. the scikit-learn documentation)
Not good for random forest: lots of 0, few 1 structured data like images, neural network might be better small data, might overfit high dimensional data, linear model might work better
Random Forest Regressor
Above we were considering random forests within the context of classification. Random forests can also be made to work in the case of regression (that is, continuous rather than categorical variables). The estimator to use for this is sklearn.ensemble.RandomForestRegressor.
Let's quickly demonstrate how this can be used:
from sklearn.ensemble import RandomForestRegressor
x = 10 * np.random.rand(100)
def model(x, sigma=0.3):
fast_oscillation = np.sin(5 * x)
slow_oscillation = np.sin(0.5 * x)
noise = sigma * np.random.randn(len(x))
return slow_oscillation + fast_oscillation + noise
y = model(x)
plt.errorbar(x, y, 0.3, fmt='o');
xfit = np.linspace(0, 10, 1000)
yfit = RandomForestRegressor(100).fit(x[:, None], y).predict(xfit[:, None])
ytrue = model(xfit, 0)
plt.errorbar(x, y, 0.3, fmt='o')
plt.plot(xfit, yfit, '-r');
plt.plot(xfit, ytrue, '-k', alpha=0.5);
As you can see, the non-parametric random forest model is flexible enough to fit the multi-period data, without us even specifying a multi-period model!
Tradeoff between simplicity and thinking about what your data is.
Feature engineering is important, need to know your domain: Fourier transform frequency distribution.
Random Forest Limitations
The following data scenarios are not well suited for random forests:
y: lots of 0, few 1
Structured data like images where a neural network might be better
Small data size which might lead to overfitting
High dimensional data where a linear model might work better


Comments