Classification (Supervised) Machine Learning Algorithms Assignment Help | Relacode4you
- realcode4you
- Dec 30, 2022
- 6 min read
Data Classification
Classification (supervised)
Decision Trees
Naïve Bayesian classifier
Time Series Analysis
Text Analysis
- Classification: assign labels to objects.
- Usually supervised: training set of
pre-classified examples.
- Our examples:
Naïve Bayesian
Decision Trees
(and Logistic Regression)
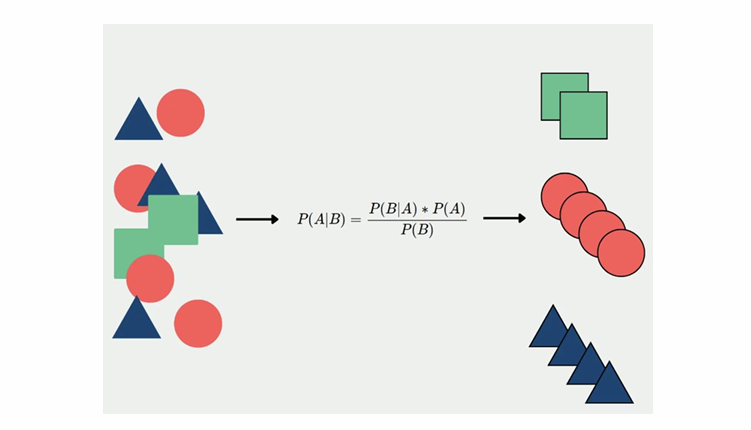
The primary task performed by classifiers is to assign labels to objects. Labels in classifiers are pre-determined unlike in clustering where we discover the structure and assign labels. Classifier problems are supervised learning methods. We start with a training set of pre-classified examples and with the knowledge of probabilities we assign class labels.
Some use case examples are shown in the slide. Based on the voting pattern on issues we could classify whether a politician has an affiliation to a party or a principle. Retailers use classifiers to assign proper catalog entry locations for their products. Most importantly the classification of emails as spam is another useful application of classifier methods.
Decision Tree Classifier - What is it?
Used for classification:
Returns probability scores of class membership
Assigns label based on highest scoring class
- Input variables can be continuous or discrete
- Output:
A tree that describes the decision flow.
Leaf nodes return either a probability score, or simply a classification.
Trees can be converted to a set of "decision rules“
"IF income < $50,000 AND mortgage_amt > $100K THEN default=T with 75% probability“
Decision Trees are a flexible method very commonly deployed in data mining applications. In this lesson we will focus on Decision Trees used for classification problems.
There are two types of trees; Classification Trees and Regression (or Prediction) Trees
Classification Trees – are used to segment observations into more homogenous groups (assign class labels). They usually apply to outcomes that are binary or categorical in nature.
Regression Trees – are variations of regression and what is returned in each node is the average value at each node (type of a step function with which the average value can be computed). Regression trees can be applied to outcomes that are continuous (like account spend or personal income).
The input values can be continuous or discrete. Decision Tree models output a tree that describes the decision flow. The leaf nodes return class labels and in some implementations they also return the probability scores. In theory the tree can be converted into decision rules such as the example shown in the slide.
Decision Trees are a popular method because they can be applied to a variety of situations. The rules of classification are very straight forward and the results can easily be presented visually. Additionally, because the end result is a series of logical “if-then” statements, there is no underlying assumption of a linear (or non-linear) relationship between the predictor variables and the dependent variable.
Decision Tree Classifier - Use Cases
When a series of questions (yes/no) are answered to arrive at a classification
Biological species classification
Checklist of symptoms during a doctor’s evaluation of a patient
Financial decisions such as loan approval
Fraud detection
An example of Decision Trees in practice is the method for classifying biological species. A series of questions (yes/no) are answered to arrive at a classification.
Another example is a checklist of symptoms during a doctor’s evaluation of a patient. People mentally perform these types of analysis frequently when assessing a situation.
Other use cases can be customer segmentation to better predict response rates to marketing and promotions. Computers can be “taught” to evaluate a series of criteria and automatically approve or deny an application for a loan. In the case of loan approval, computers can use the logical “if-then” statements to predict whether the customer will default on the loan. For customers with a clear (strong) outcome, no human interaction is required, for observations which may not generate a clear response, a human is needed for the decision.
Short Decision Trees (where we have limited the number of splits) are often used as components (called "weak learners" or "base learners") in ensemble techniques (a set of predictive models which will all vote and we take decisions based on the combination of the votes) such as Random forests, bagging and boosting (Beyond the scope for this class). The very simplest of the short trees are decision stumps: Decision Trees with one internal node (the root) which is immediately connected to the terminal nodes. A decision stump makes a prediction based on the value of just a single input feature.
Step 1: Pick the Most “Informative" Attribute
- Entropy-based methods are one common way

- H = 0 if p(c) = 0 or 1 for any class
So for binary classification, H=0 is a "pure" node
- H is maximum when all classes are equally probable
For binary classification, H=1 when classes are 50/50
The first step is to pick the most informative attribute. There are many ways to do it. We detail Entropy based methods.
Let p( c ) be the probability of a given class. H as defined by the formula shown above will have a value 0 if p (c ) is 0 or 1. So for binary classification H=0 means it is a “pure” node. H is maximum when all classes are equally probable. If the probability of classes are 50/50 then H=1 (maximum entropy).
Information Gain

The information that you gain, by knowing the value of an attribute
So the "most informative" attribute is the attribute with the highest InfoGain
Information gain is the amount of information gained by knowing the value of the attribute
Information gain= (Entropy of distribution before the split)–(entropy of distribution after it)Information Gain is defined as the difference between the base entropy and the conditional entropy of the attribute.
So the most informative attribute is the attribute with most information gain. Remember, this is just an example. There are other information/purity measures, but InfoGain is a fairly popular one for inducing Decision Trees.
Weather data

Steps to calculate the highest information gain on a data set
Step 1: Calculate Entropy for whole dataset:
Entropy of the whole data set
14 records, 9 are “yes” 5 are “no”

Step 2: Calculate Entropy for each attribute:
The outlook attribute contains 3 distinct values:
- overcast: 4 records, 4 are “yes”

- rainy: 5 records, 3 are “yes”

- sunny: 5 records, 2 are “yes”

Expected new entropy:

Step 3: Calculate Information gain for each attribute:
Attribute1 - outlook
Gain

Diagnostics
- Hold-out data
- Confusion Matrix
- FPR/FNR, Precision/Recall
- Do the splits (or the "rules") make sense?
What does the domain expert say?
- How deep is the tree?
Too many layers are prone to over-fit
- Do you get nodes with very few members?
Over-fit
We use the hold-out data /AUC and confusion matrix for diagnostics. There are sanity checks that can be performed such as validating the “decision rules” with domain experts and determining if they make sense.
Having too many layers and obtaining nodes with very few members are signs of over fitting.
Diagnostics: Confusion Matrix

A confusion matrix is a specific table layout that allows visualization of the performance of a model. In the hypothetical example of confusion matrix shown:
Of 1000 credit score samples, the system predicted that there were good and bad credit, and of the 700 good credits, the model predicted 29 as bad and similarly 38 of the actual bad credits were predicted as good. All correct guesses are located in the diagonal of the table, so it's easy to visually inspect the table for errors, as they will be represented by any non-zero values outside the diagonal.
We define overall success rate (or accuracy) as a metric defining – what we got right - which is the ratio between the sum of the diagonal values (i.e., TP and TN) vs. the sum of the table. In other words, the confusion table of a good model has large numbers diagonally and small (ideally zero) numbers off-diagonally.
We saw a true positive rate (TPR) and a false positive rate (FPR) when we discussed ROC curves:
TPR – what percent of positive instances did we correctly identify.
FPR – what percent of negatives we marked positive.
Additionally we can measure the false negative rate (FNR):
FNR– what percent of positives we marked negative
The computation of TPR, FPR and FNR are shown in the slide.
Precision and Recall are accuracy metrics used by the information retrieval community; they are often used to characterize classifiers as well. We will detail these metrics in lesson 8 of this module.
Note:
precision – what percent of things we marked positive really are positive
recall – what percent of positive instances did we correctly identify. Recall is equivalent to TPR.


Comments